Image

Concepts it verify

CIRCLE THEOREMS

Su-Art-CT-01-20

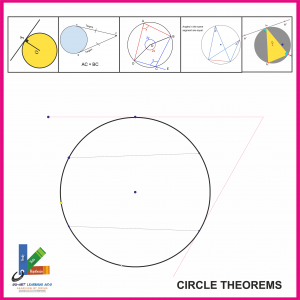
• 1. Radius tangent theorem
• 2. Two tangent theorem
• 3. Angle subtended by the arc at the centre
• 4. Angles subtended by the same arc at circumference
• 5. Tangent Chord theorem
• 6. Cyclic quadrilateral theorem

PYTHAGORAS / AREA THEOREMS

Su-Art-PAT-02-20

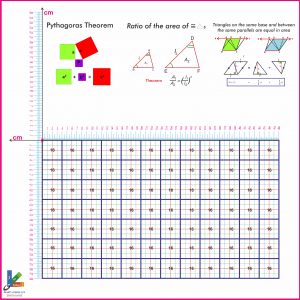
• 1. Pythagoras theorem
• 2. Ratio of area of triangle theorem
• 3. Determining the area of triangle with same altitude
• 4. Verifying that the area of triangle is half the parallelogram on the same base
• 5. Verifying the parallelograms has the same area if the base is same

ESTIMATING 'PI'

Su-Art-PI-03-20

• 1. Estimating ‘Pi’ with two methods
• [1.1] Thread method
• [1.2] Rotation method

PARALLEL LINES / TRIANGLE PROPERTIES

Su-Art-PTP-04-20

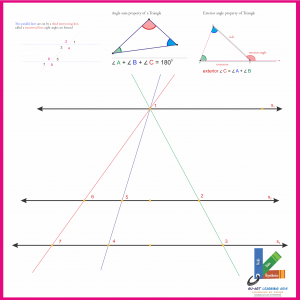
• 1. Opposite angle theorem (For pair of line segment intersecting)
  
• 2. Parallel line theorem
• [a] Corresponding angles
• [b] Interior alternate angles
• [c] Interior alternate angles on the same side
• [d] Interior alternate angles on the same side
  
• 3. Checking for the parallel lines
  
• 4. Exterior angle of a triangle and its properties
• [a] For Acute angle triangle
• [b] For obtuse angle triangle
• [c] For Right angle triangle
  
• 5. Angle sum property of the triangle
• [a] For Acute Angle triangle
• [b] For Obtuse angle triangle
• [c] For right angle triangle

REPRESENTING ROOT 'X'

Su-Art-RX-05-20

• 1. Determining the value of ‘√x’ on the number line

SIMILARITY Vs CONGRUENCE

Su-Art-SC-06-20

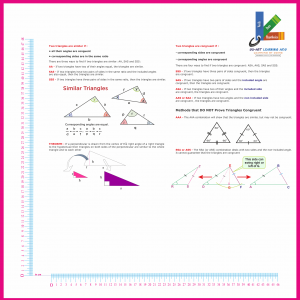
• 1. Verifying for congruence (Triangle Cut-out demonstration)
• [1.1] SSS
• [1.2] SAS
• [1.3] ASA
• [1.4] AAS or SAA
  
• 2. Verifying Method that do not prove triangles are congruent (Triangle Cut-out demonstration)
• [2.1] AAA
• [2.2] SSA or ASS
  
• 3. Verifying for similarity
• [3.1] AA
• [3.2] SAS
• [3.3] SSS
  
• 4. Similar triangle theorem – Perpendicular drawn from the vertex of right angle... (Triangle cut-out demonstration)

ARITHMETIC PROGRESSION

Su-Art-AP-08-20

• 1. Verification that first ‘n’ natural numbers can be represented as rectangle
• 2. Verification that the first ‘n’ natural odd numbers can be represented as perfect square

BASIC PROPORTIONALITY / TRIANGLE THEOREM

Su-Art-BPTT-07-20

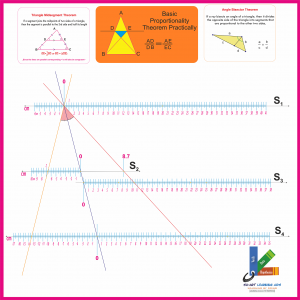
• 1. Triangle mid-segment theorem
• 2. Basic proportionality theorem
• 3. Angle bisector theorem
• 4. Triangle properties
• [a] Demonstrating equilateral triangle theorem
• [b] Side opposite to the greater angle in a triangle is always greater.
• [c] Sum of the two sides of the triangle is greater than the third side.

TRIGONOMETRIC IDENTITIES

Su-Art-TI-09-20

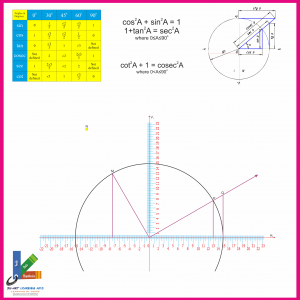
• 1. The value of sineθ increases as ‘θ’ increases
• 2. The value of cosθ decreases as ‘θ’ increases.
• 3. The value of trigonometry ratios do not vary with lengths of the sides of the triangle, if the angle remains the same.
• 4. Verifying –
• [a] cos²A + sin²A = 1
  [b] 1 + tan²A = sec²A
  [c] cot2A + 1 = cosec2A

NUMBER OPERATIONS

Su-Art-NO-10-20

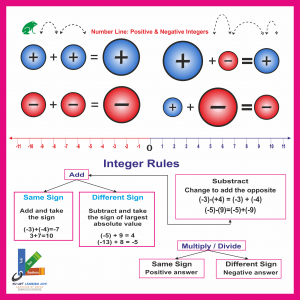
• 1. Addition of integers (positive and negative) over the number line. All cases have been explored.
• a) Addition of two integers having the same sign
• b) Addition of two integers having different signs
  
• 2. Subtraction of integers over the number line
• a) Subtraction of two integers either of them of both have the same sign.
  
• 3. Multiplication of integers over number line
• a) Multiplication of two integers having same sign.
• b) Multiplication of two integers having different sign

We design and manufacture Mathematical apparatus kits and establish Math labs.

We design and manufacture Mathematical apparatus kits and establish Math labs.

POLYGON / QUADRILATERAL PROPERTIES

Su-Art-PQP-11-20

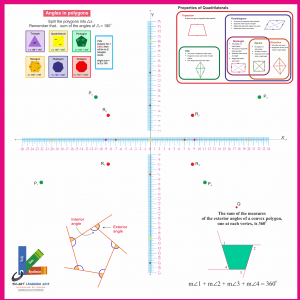
• 1. Angle sum property of a polygon
• 2. Exterior angle property of a polygon
  
• 3. Exploring kind of quadrilateral and their properties
• a) Exploring all squares are rhombus
• b) Exploring similarity and dissimilarity in kite and rhombus.
• c) Exploring similarities and differences in the properties with respect to diagonals of the quadrilaterals – a parallelogram, a square, a rectangle, a kite and a rhombus.
• d) Exploring figure obtained by joining the mid-points of consecutive sides of the quadrilateral

ALGEBRAIC IDENTITIES

Su-Art-AI-12-20

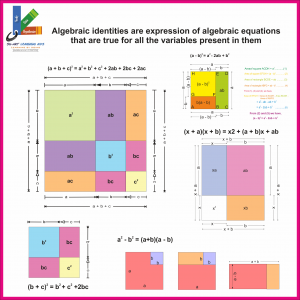
• 1. Modelling Identity I: (a + b)² = a² + 2ab + b²
• 2. Modelling Identity II: (a – b)² = a²– 2ab + b²
• 3. Modelling Identity III: a² – b² = (a + b)(a – b)
• 4. Modelling Identity IV: (x + a)(x + b) = x² + (a + b) x + ab
• 5. Modelling Identity V: (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
  

FRACTION OPERATIONS

Su-Art-FO-13-20

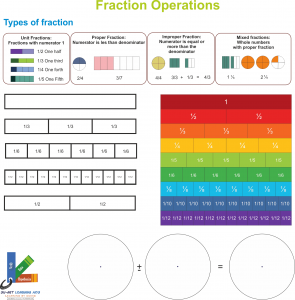
• 1. Modelling fractions
• [a] Modelling proper fractions
• [b] Modelling improper fractions and mixed fractions
• [c] Modelling fractions equivalent to one (1)
• [d] Modelling equivalent fractions
  
• 2. Operations over fractions
• [a] Summation operation with circular fractions / bar fractions
• [b] Subtraction operation with circular fractions / bar fractions.

TRIANGLE CENTRES

Su-Art-TC-14-20

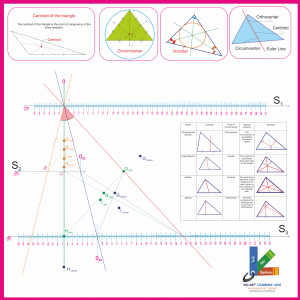
• 1. Exploring and identifying the following triangle centres with respect to ‘Acute triangle’, ‘Right triangle’, ‘Obtuse triangle’
• [a] Incentre (I)
• [b] Orthocentre (H)
• [c] Centroid (G) and its property
• [d]Circumcenter (O)
  
• 2. Exploring Euler line and its property

DIRECT AND INVERSE PROPORTION

Su-Art-DIP-15-20

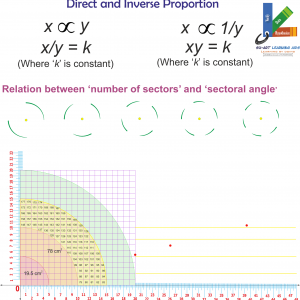
• 1. Exploring inverse proportional relationship between the two variables
• [a] Exploring relation between number of sectors and sectorial angle
  
• 2. Exploring direct proportional relationship
• [a] Exploring relationship between circle’s circumference and its diameter
• [b] Relationship between ‘base’ and ‘height’ for similar right triangles
• [c] Relationship between the ‘Area of quarter circle’ and its ‘radius’

SIMPLE INTEREST / COMPOUND INTEREST

Su-Art-SCI-16-20

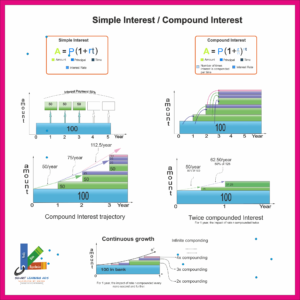
• 1. Deducing Simple Interest.
• 2. Deducing Compound Interest and comparing it with 'Simple Interest' for 'same period', 'equal Principal amount' and 'equal annual rate of interest'.